(zfklkfz) TEORÍA AERODINÁMICA DE LA RELATIVIDAD

TEORIA AERODINÁMICA DE LA RELATIVIDAD

 

INTRODUCCIÓN

 

Hay dos maneras de analizar una idea novedosa;

la más usual es cotejar esta idea con la verdad

oficial y si no coincide con ella arrojar a la

hoguera del kulturcampf o de la Inquisición

dicha novedad.

 

La otra forma es suponer que quizás haya algo de

cierto en la nueva idea e, incluso, pensar que

la verdad oficial puede contener errores;

después de todo la teoría geocéntrica de Ptolomeo

fue la verdad oficial para muchos astrónomos

durante muchos siglos.

 

El siguiente trabajo va dirigido a quienes sean capaces

de pensar de la segunda manera, esperando que

puedan ampliar mi teoría ya que tal como la expongo

está necesariamente limitada para hacerla comprensible

a la mayor cantidad de lectores. Podemos decir que,

tal como está, es solo el primer capítulo de un libro

que todavía no se escribe.

Así pues, queda en las manos de estos lectores

la corroboración y ampliación de la teoría.

Algunas de las ideas son solo especulaciones

en las que habrá que profundizar.

 

Estudié Ingeniería Aeronáutica en la Escuela Superior de Ingeniería Mecánica y Eléctrica (ESIME) del Instituto Politécnico Nacional de México. Durante más de treinta años combiné mi actividad como catedrático en dicha escuela con mi trabajo en diversas empresas aéreas. Actualmente estoy jubilado.

 

Al jubilarme, decidí aprovechar mi tiempo en completar mis conocimientos, tratando de contestar a muchas dudas que, como estudiante y/o profesionista, no tuve tiempo de analizar y responder, por falta de tiempo.

 

Entre las primeras dudas que me planteé surgieron algunas relacionadas con la Teoría de la Relatividad de Einstein y su semejanza con las leyes de la aerodinámica.

 

Al profundizar en este tema, llegué a la conclusión de que la Teoría de la Relatividad de Einstein se puede explicar de una manera mas facil y afín con las concepciones normales de la gente común, por medio de las leyes de la Aerodinámica. Este es el objeto del siguiente trabajo.

 

Para hacerlo mas entendible al mayor número de personas, he reducido al mínimo los tratamientos matemáticos y el lenguaje técnico; por ejemplo, uso la palabra fórmula para referirme a lo que, en rigor, es una ecuación, consciente del hecho de que esta inexactitud es mas entendible por la mayoría de la gente; también prescindo del lenguaje normal de las matemáticas y escribo las fórmulas con palabras completas y utilizo signos de multiplicación que son totalmente innecesarios en el lenguaje normal del álgebra elemental. También introduzco dibujos que resultan innecesarios para quienes están familiarizados con la física y defino características que no son del uso común entre los no especializados.

 

No obstante, estas simplificaciones no le quitan rigor matemático y físico a lo aquí expuesto. Quienes  tengan conocimientos de física y matemáticas no tendrán ningún problema en identificar como ecuaciones diferenciales lo que yo llamo formas diferenciales y podrán utilizar todos sus conocimientos para desarrollar los planteamientos físico-matemáticos de una manera más completa y adecuada de la que yo uso.

 

Con estas limitaciones pretendo hacer accesible este trabajo a cualquier persona que tenga una escolaridad mayor o igual a la de estudios secundarios. Para quienes no tengan este nivel, este trabajo será difícil o incomprensible, pero creo que para los demás será bastante accesible.

 

El trabajo está dividido en varias secciones:

 

En la primera sección desarrollo una serie de conocimientos que tienen que ver con la Teoría Aerodinámica normal que se utiliza en el cálculo de aviones.

 

En la segunda sección esbozo la Teoría Restringida de la Relatividad de Einstein, sin entrar en muchos detalles.

 

En la tercera sección comparo ambas teorías y doy mis razones para considerar más válida la teoría aerodinámica que la de Einstein.

 

En una cuarta sección hablo brevemente de la Teoría Generalizada de la Relatividad y expongo una posible corrección a la misma.

 

 

 

 

Agradeceré cualquier comentario, corrección o ampliación en las siguientes direcciones:

 

Ing. Carlos Ordóñez Garcia.

Condominio Tepec. Lote 58.

Calle de los Doctores 29.

Jiutepec. Morelos.

México.

 

E-mail: "cog1937@yahoo.com"

 

 

 

 

 

 

AERODINÁMICA

 

LOS FLUIDOS.

 

Como este libro va dedicado a personas que posiblemente no tienen conocimientos de física, recordaré que todos los cuerpos están formados por partes muy pequeñas a las que llamaremos corpúsculos. Los corpúsculos en algunos casos son átomos y en otros son moléculas, pero siempre son muy pequeños.

 

Los cuerpos pueden ser sólidos, líquidos o gases.

 

En los sólidos los corpúsculos están fuertemente unidos entre si y por ello los sólidos conservan su forma y hay que aplicar fuerzas grandes para deformarlos.

 

Los líquidos y los gases cambian fácilmente de forma, por lo que se dice que son fluidos.

 

En los líquidos los corpúsculos están débilmente unidos y se mueven cambiando de posición pero sin separarse. Podemos imaginar un líquido como un conjunto de canicas en una caja, si cambiamos la posición de la caja, las canicas ruedan hacia los lugares mas bajos.

 

Los corpúsculos en los gases no están unidos y se mueven libremente en todas direcciones ocupando todo el espacio del recipiente en que se encuentran. En lo que sigue hablaremos sobre todo de gases, por lo que es importante que el lector se haga la idea de un gas como un conjunto de cosas muy pequeñas (corpúsculos)  moviéndose en todas direcciones y chocando contra las paredes del recipiente que contiene el gas. Algo así como un enjambre de moscas dentro de un frasco.

 

De acuerdo con esta analogía, si ponemos en el frasco un tapón que pueda  bajar (émbolo), las moscas tendrán menos espacio para volar y chocaran más veces con las paredes, es decir el gas está comprimido y ocupa menos volumen.

 

Pero si llenamos el frasco con canicas y tratamos de bajar el émbolo, no podremos, es decir el líquido no se puede comprimir.

 

Esta es una característica que distingue a los líquidos de los gases. Los líquidos son fluidos incompresibles mientras que los gases son fluidos compresibles.

 

El comportamiento de líquidos y gases es muy parecido y se explica por leyes físicas semejantes, pero no es idéntico. Si aplicamos las leyes y ecuaciones de la hidráulica (líquidos) al estudio de un gas obtendremos resultados equivocados. Para conseguir resultados correctos tenemos que usar las leyes y ecuaciones de la aerodinámica.

 

 

FLUIDOS EN REPOSO

 

LA ENTALPÍA.

 

Si calentamos un frasco con émbolo que contiene gas observamos dos cosas: la temperatura del gas aumenta y el émbolo sube, es decir el gas aumenta de volumen (se dilata).

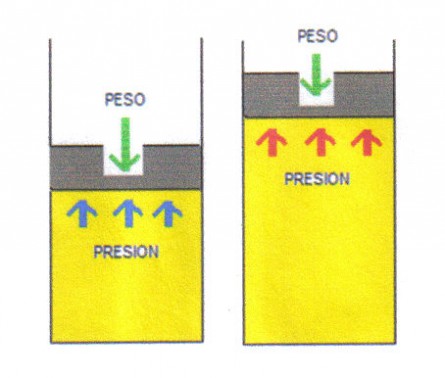
Podemos decir que el calor entra al gas y queda atrapado en él, o más exactamente en los corpúsculos que lo forman y que se moverán a mayor velocidad. Pero una parte del calor se emplea en empujar el émbolo y hacer que el gas aumente de tamaño.

 

Para ser mas claro: el calor aplicado al frasco se separa en dos partes: una que aumenta la temperatura y otra que aumenta el volumen.

 

El calor total, o sea la suma de estas dos partes, se llama entalpía.

 

Por nuestra experiencia diaria sabemos que mientras mas calor apliquemos mayor será la temperatura y mayor la expansión del gas, pero también sabemos que mientras mayor sea la masa de gas mas calor necesitaremos para subir la temperatura. Matemáticamente esto se expresa por la relación:

 

Calor = C_P x Masa x Temperatura

 

O mas adecuadamente:

 

Entalpía  = C_P x Masa x Temperatura

 

Utilizamos la abreviatura C_P para referirnos al Calor específico a presión constante.

 

El calor específico es un número que depende del material que estemos calentando y decimos que es a presión constante porque, en efecto, si observamos la figura anterior vemos que el émbolo tiene un peso y que éste está contrarrestado por la presión del gas. Como el peso no cambia, la presión tampoco y por lo tanto la dilatación del gas se hace a presión constante, lo que justifica el nombre de calor específico a presión constante.

 

En realidad el calor que aplicamos al gas se añade al calor que tenía anteriormente, por lo que es más correcto hablar de una variación del calor y una variación de la temperatura, que también pasa de un valor a otro. Dicho en otras palabras, lo correcto es escribir:

 

Variación de Entalpía  = C_P x Masa x Variación de Temperatura 

 

Al escribir la formula de las variaciones de este tipo, la ecuación correspondiente se llamará forma diferencial. La última ecuación es, por lo tanto, la forma diferencial de la entalpía.

 

 

 

Hagamos otro experimento.

 

En lugar del frasco con émbolo pondremos el gas en un recipiente totalmente cerrado, por ejemplo una olla express. En este caso todo el calor se usará para aumentar la temperatura y nada para aumentar el volumen. Pero ahora la presión dentro de la olla aumenta.

 

Otra vez nos encontramos con que el calor total (o sea la entalpía) se divide en dos partes: una para elevar la temperatura y otra para aumentar la presión.

 

Comparando los dos casos vemos que en ambos hay una parte del calor que sirve para aumentar la temperatura y en cada uno de ellos hay otra parte que en un caso se utiliza para aumentar el volumen (manteniendo la presión constante) y en el otro se utiliza para aumentar la presión (manteniendo el volumen constante).

 

Ya dijimos que el calor (que es una forma de energía) empleado para aumentar la temperatura es absorbido por las moléculas del gas haciendo que estas se muevan mas rápido. O lo que es lo mismo, esta energía se encuentra dentro del gas, lo que justifica que la llamemos energía interna del gas.

 

Su valor se puede calcular con la fórmula:

Energía Interna = C_V x Masa x Temperatura

Donde C_V es una abreviatura para referirnos al calor específico a volumen constante, que es un número que depende de la sustancia que se esté calentando.

La forma diferencial de esta ecuación es:

Variación de Energía Interna = C_V x Masa x Variación de Temperatura

Como se ve fácilmente las fórmulas de la entalpía y de la energía interna son casi iguales y dependen de la masa y la temperatura.

 

La otra parte de la energía se utiliza para modificar las condiciones del recipiente, aumentando el volumen en un caso o la presión en el otro. A esta parte de la energía la podríamos llamar energía del recipiente.

 

Entonces podemos concluir que:

 

VARIACIÓN DE ENTALPÍA = VARIACIÓN DE ENERGÍA INTERNA + VARIACIÓN DE ENERGÍA DEL RECIPIENTE

 

 

Hablemos un poco más sobre la energía  del recipiente.

Es fácil demostrar que la energía utilizada para aumentar el volumen del gas manteniendo la presión constante se calcula por:

 

Variación de Energía del recipiente = Presión  x  Variación de Volumen

 

Y que la energía utilizada para aumentar la presión del gas manteniendo el volumen constante se puede calcular por:

 

Variación de Energía del recipiente = Volumen  x  Variación de Presión

 

Estas dos fórmulas se pueden relacionar con lo que se conoce como Ecuación de los Gases Perfectos, que muchos lectores conocen, y que dice:

 

Presión x  Volumen = R x Masa x Temperatura

 

Donde el número  R  es un valor que se conoce como Constante Universal de los Gases.

 

La Ecuación de los Gases Perfectos se puede escribir en su forma diferencial como:

 

(Presión  x  Variación de Volumen) + (Volumen  x  Variación de Presión) =  R x Masa  x  Variación de Temperatura  

En el primer caso que vimos, como no hay variación de presión, ésta es cero y solo nos queda la multiplicación de Presión x Variación de volumen. En el segundo, la variación de volumen es cero y solo queda Volumen x Variación de Presión. Por lo que en ambos podemos decir que:

 

Variación de Energía del recipiente = (Presión  x  Variación de Volumen) + (Volumen x Variación de Presión)

 

Ya que en cada caso uno de los sumandos es cero y solo queda el otro.

 

Pero, además, considerando la Ecuación de los Gases Perfectos:

Variación de Energía del recipiente = Masa  x  Variación de Temperatura  x  R

Y recordando que la variación de entalpía es la suma de las otras dos:

C_P x Masa x Variación de Temperatura = C_V x Masa x Variación de Temperatura  + R x Masa  x  Variación de Temperatura 

 

 

Como en las tres energías aparecen la masa y la variación de temperatura, lo único distinto entre ellas son las constantes y, por lo tanto podemos decir que:

C_P = C_V + R

 

Para la mayoría de los lectores que tengan estudios de preparatoria o superiores casi todo lo expuesto hasta aquí les debe ser conocido y si hacen memoria lo recordaran.

Para quienes solo hayan estudiado secundaria quizás les resulten desconocidas las consideraciones físicas, aunque en su experiencia diaria deben haberse encontrado con casos de calentamiento de gases similares a los descritos aquí, por lo que no pienso que les sea difícil concebir y comprender lo que he dicho. Las matemáticas empleadas son muy sencillas y casi lo único que se requiere es saber interpretar una multiplicación en la que se usan palabras en lugar de números (en problemas específicos las palabras se substituyen por los números correspondientes al problema).

Espero que todo lo anterior haya quedado relativamente claro para la mayoría de los lectores y lamento no poder reducir más los planteamientos matemáticos, pero… así es esto de la física. Las matemáticas nos permiten medir, cuantificar y predecir los resultados de un experimento físico.

Resumiendo:

La entalpía (calor total que se aplica a un gas) produce cambios en la presión, el volumen y la temperatura del gas y estos cambios son más o menos notables dependiendo de la masa del gas.

Por último, muchas veces es mas conveniente estudiar lo que ocurre en una unidad de volumen y para ello, en las ecuaciones anteriores el volumen siempre será igual a 1 y la masa se sustituirá por la densidad, que es la cantidad de masa (cantidad de corpúsculos) que caben en un volumen determinado o lo que es lo mismo:

Densidad = Masa / Volumen

En lo que sigue veremos una aplicación de esto.

 

EL CAMBIO ADIABÁTICO

En el capítulo anterior vimos lo que le ocurre a un gas al ser calentado a presión o a volumen constantes. Ahora veremos otro proceso de cambio de un gas en el que no se aplica calor, pero que conlleva un cambio en la presión y la temperatura. Volvamos a nuestro recipiente con émbolo y supongamos que aumentamos la presión, por ejemplo colocando unas pesas sobre el émbolo, Al aumentar el peso sobre el gas aumenta la presión y el gas se comprime (disminuye su volumen). Al mismo tiempo aumenta su temperatura.

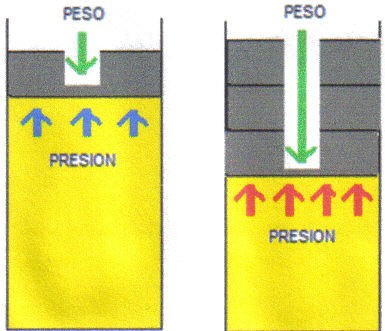
Esto es lo que ocurre, por ejemplo, al usar una bomba para inflar la llanta de una bicicleta; el gas se comprime y al mismo tiempo se calienta. Otro ejemplo, quizás más notable, es el caso inverso cuando el gas se expande y baja su temperatura, como en el caso de una corriente de aire; cuando hay viento sentimos más frío que cuando no lo hay porque el aire se expande y baja su temperatura.

El gas se comprime y se calienta por el aumento de la presión o se expande y se enfría por la disminución de presión, aunque no se le está aplicando fuego. La palabra adiabático significa que no se aplica calor.

La ecuación que relaciona la temperatura con la densidad del gas en un proceso adiabático es:

Temperatura = Densidad^(R/Cv)  x  un número constante

Seguramente muchos lectores recordarán de sus cursos de química o física una fórmula equivalente a la anterior en la que se relacionan el volumen y la presión: Presión x Volúmen^CP/CV  = constante. En este estudio nos será de más utilidad la formula que relaciona la temperatura con la densidad.

La forma diferencial de esta ecuación es:

Variación de Temperatura / Temperatura inicial =

(R/C_V)  x  (Variación de Densidad / Densidad inicial)

Y como la densidad es la masa que hay en una unidad de volumen, podemos concluir que:

Variación de Temperatura =

Temperatura inicial x (R/C_V)  x  (Variación de Masa / Masa inicial)

Todo lo anterior nos ha servido para definir las relaciones entre presión, volumen, temperatura y calor de un gas; y para distinguir entre entalpía, energía interna y energía del recipiente (presión x volumen) de un gas. Lo importante no son las fórmulas sino la concepción de los hechos. Creo que los ejemplos dados dan bastante claridad sobre la forma en que se comporta un gas al calentarlo o al comprimirlo sin aplicarle fuego y estoy seguro que muchos lectores han visto casos similares en su experiencia diaria, aunque no hayan cuantificado los cambios de presión, temperatura, etc. y menos aun hayan establecido fórmulas matemáticas para medirlos. Lo importante, repito, es la concepción del hecho. Las fórmulas solo nos dan una forma de medir lo que hemos observado. No obstante, las fórmulas nos permiten calcular lo que sucede y, por lo tanto, medir los cambios de las cantidades estudiadas.

Todas las fórmulas anteriores nos han servido para aclarar nuestros conceptos y para definirlos con precisión; para tener una idea clara de ellos. Pero, de todo lo anterior, lo único que necesitamos en lo que sigue es entender  con claridad la forma diferencial de la transformación adiabática, esta será la clave para lo que sigue, pero para entenderla fue necesario todo lo anterior.

 

EL SONIDO

Cuando un sólido se mueve en un fluido (por ejemplo cuando una lancha avanza por un lago o cuando, al golpear la membrana de un tambor, ésta se desplaza), el sólido empuja los corpúsculos del fluido que entran en contacto con él y los comprime. Para descomprimirse, estos corpúsculos, a su vez, empujan a los que están en sus alrededores y los comprimen, y así sucesivamente formando una onda que avanza por el fluido comprimiendo capas del mismo cada vez mas alejadas del sólido que las originó.

Aunque, en un principio, la onda se creó por el empuje del sólido sobre el fluido, la transmisión posterior se debe solo a las interacciones entre corpúsculos de capas adyacentes del mismo fluido y ya no depende del sólido. La velocidad con que se comprimen o descomprimen las capas depende exclusivamente de las características del fluido. Cuando una de estas ondas llega a nuestros oídos percibimos un sonido por lo que a estas ondas las llamamos ondas sonoras y la velocidad con que avanzan es la velocidad del sonido.

Un ejemplo muy típico de esto son las ondas que se forman cuando tiramos una piedra en un estanque.

Por otra parte, como no hay adición de calor, la compresión y descompresión de las capas sucesivas es claramente un proceso adiabático. En el caso de los gases la velocidad del sonido viene expresada por la fórmula:

 

c² = C_P x R x Temperatura / C_V

 

Aquí hemos utilizado la letra c para referirnos a la velocidad del sonido. Si hacemos el cálculo y obtenemos la raíz cuadrada de c, tendremos el valor de la velocidad del sonido, que, como vemos, depende de los valores constantes de los calores específicos y la constante universal de los gases y del valor (variable) de la temperatura del gas.

 

 

 

RELACIÓN ENTRE ENTALPÍA Y VELOCIDAD DEL SONIDO EN UN CAMBIO ADIABÁTICO.

 

Ya dijimos que la forma diferencial de la entalpía es:

 

Variación de Entalpía  =  C_P  x Masa  x  Variación de Temperatura

 

Pero también vimos que la relación entre temperatura y densidad en un cambio adiabático es:

 

Variación de Temperatura =

Temperatura inicial x (R/C_V)  x  (Variación de Masa / Masa inicial)

 

Esta relación depende de los valores iniciales (antes de la compresión), por lo que recordaremos esto y quitaremos la palabra “inicial” de nuestras fórmulas. Sustituyendo la Variación de Temperatura en la formula de la entalpía tendremos:

Variación de Entalpía = 

C_P x Masa x Temperatura x (R/C_V)  x (Variación de Masa / Masa)

Que, simplificando, se reduce a:

Variación de Entalpía =  (C_P x R/C_V)  x Temperatura x Variación de Masa

Pero también hemos visto que la cantidad: (C_P x R/C_V)  x Temperatura es el valor del cuadrado de la velocidad del sonido (c²) por lo que finalmente tendremos.

Variación de Entalpía = c² x Variación de Masa

 

Recordemos que nos estamos refiriendo a lo que pasa en una unidad de volumen.

 

 

 

 

FLUIDOS EN MOVIMIENTO

 

MOVIMIENTO RELATIVO

 

Comenzaremos por considerar lo que se puede llamar Primer Principio del Movimiento Relativo que establece que si un cuerpo se mueve con respecto a uno en reposo los fenómenos físicos son iguales a los que observaríamos si el cuerpo móvil estuviera en reposo y fuera el otro el que se moviera. Dicho en otras palabras: si un avión se mueve de Norte a Sur a través del aire en calma  es lo mismo que si el avión estuviera fijo y el aire se moviera de Sur a Norte.  Igualmente, si corremos rápido en una bicicleta decimos que el aire (el viento) golpea muestra cara, cuando en realidad el aire esta quieto y es nuestra cara la que lo golpea.

 

Este Principio es muy útil pues nos permite intercambiar lo que está fijo y lo que se está moviendo para estudiar lo que ocurre. Por ejemplo, en aviación se estudia el movimiento de los aviones en túneles de viento que son túneles por los que circula aire a cierta velocidad al que se hace pasar por un modelo del avión, montado rígidamente dentro del túnel y al que se le conectan aparatos de medida. Así resulta fácil medir fuerzas, energías, etc. sin necesidad de ensayar de verdad con un avión real en el que sería más difícil hacer las mediciones y con el que correríamos el riesgo de que se cayera y se matara el piloto. Los resultados obtenidos de esta forma son los mismos que encontraríamos, con más riesgos y más gastos, si el avión volara en un aire en calma a la misma velocidad con la que se mueve el aire en el túnel.

 

Casi siempre, no solo en aviación, resulta más fácil considerar que el fluido se mueve y que el cuerpo que estudiamos está fijo.

 

 

MOVIMIENTO DE UN CUERPO DENTRO DE UN FLUIDO

 

 

Cualquier cuerpo que tiene movimiento relativo con respecto a un fluido en el que está sumergido produce una deformación del mismo en su proximidad, independientemente de que se mueva el cuerpo y el fluido esté en reposo o viceversa. Es decir hay una alteración local en las velocidades y presiones del fluido. Una vez que pasa el cuerpo, el fluido vuelve a las condiciones que tenía antes de ser alterado. En la zona alterada, el fluido aumenta su  velocidad y se alarga en el sentido de la velocidad al mismo tiempo que se contrae en el sentido longitudinal.

Si el fluido es incompresible (líquido) los cambios son pequeños y podemos decir que conserva la misma forma en la región alterada y en la región sin alterar.

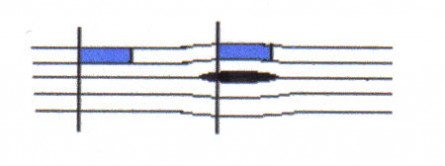
                        Sección 0                      Sección 1       

 

Tamaño y forma de una unidad de masa de fluido incompresible en la región sin perturbar (Sección 0) y en la región perturbada (Sección 1).

 

 

Si el fluido es compresible (gas) hay además una compresión en el sentido del movimiento, de modo que la forma cambia notablemente, reduciéndose las distancias entre partículas en la dirección del movimiento.

 

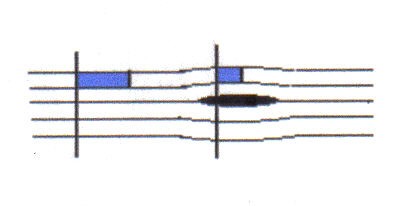
                        Sección 0                      Sección 1       

 

Tamaño y forma de una unidad de masa de fluido compresible en la región sin perturbar (Sección 0) y en la región perturbada (Sección 1).

 

 

 

De acuerdo con esto, si una unidad de masa de un líquido y otra de un gas ocupan el mismo volumen en la zona sin perturbar, se verán idénticas; pero en la zona perturbada, debido a la compresión, el gas ocupa menos volumen, o lo que es lo mismo, hay más gas en el mismo volumen. Ya dijimos que el líquido se mantiene prácticamente igual en la zona perturbada y sin perturbar.

 

Esto se ejemplifica en la figura siguiente en la que vemos que el cuerpo sumergido en un líquido está en contacto con menos unidades de masa (2 Kg.) que el que se encuentra en un fluido compresible (3 Kg.)

                                    Líquido.                                                       Gas.

 

 

 Cantidad de masa que rodea a un mismo cuerpo.

 

 

Podemos suponer que estas masas están encerradas en recipientes del mismo volumen y por lo tanto la velocidad del recipiente determina la velocidad de su contenido. Como el volumen y la velocidad de los recipientes son iguales, ambos volúmenes recorren distancias iguales en tiempos iguales (a esto se le llama gasto volumétrico en hidráulica). Pero la cantidad de masa que pasa sobre el cuerpo en cierto tiempo es diferente (2 Kg. de líquido o 3 Kg. de gas), a esto se le llama gasto másico.

 

Esta diferencia de masas hace que los valores de las magnitudes físicas sean diferentes; por ejemplo, la energía cinética es:

 

Energía Cinética = Masa x Velocidad²  / 2

 

Como la velocidad de los dos recipientes es la misma, la energía depende solo de la masa (2 Kg. de líquido o 3 Kg. de gas), por lo que la energía del gas es mayor que la del líquido.

 

Lo mismo sucede con las fuerzas; si aplicamos la segunda ley de Newton:

 

Fuerza = Masa x Aceleración

 

La fuerza que ejerce el gas sobre el cuerpo es mayor que la que ejerce el líquido.

 

Esto último puede chocar al lector, que sabe por experiencia que las fuerzas y energías de un líquido son mayores a las de un gas; pero debemos recordar que partimos de la suposición de que ambos tenían la misma densidad, o sea que la misma masa ocupaba el mismo volumen. En la realidad los líquidos son mucho más densos que los gases.

 

 

 

 

 

ENERGÍA TOTAL DE UN FLUIDO EN MOVIMIENTO.

 

Un gas en movimiento tiene una entalpía que depende de su temperatura, lo mismo que cuando está en reposo; pero además tiene una energía debida a su movimiento, esta energía se llama energía cinética y se mide por la conocida fórmula:

Energía Cinética = Masa x Velocidad²  / 2

Tanto la entalpía como la energía cinética son energías y por consiguiente si las sumamos tendremos la energía total de un gas en movimiento y vemos que está constituida por una parte debida a su temperatura (entalpía) y otra debida a su velocidad (energía cinética).

Energía Total = Entalpía + Energía Cinética

Aclararemos esto con un ejemplo sencillo. Supongamos un tanque de aire comprimido. Este gas no está en movimiento, por lo que su energía cinética es cero, pero tiene una entalpía resultado de su proceso de compresión. En este caso la energía total es igual a la entalpía del gas comprimido:

Energía Total = Entalpía_COMPRIMIDO

Si abrimos el tanque, el gas se escapa formando una corriente de cierta velocidad y al mismo tiempo se descomprime hasta que su presión sea igual a la atmosférica; en esta descompresión disminuye la entalpía, pero debido al movimiento hay una energía cinética, por lo que tendremos:

Energía Total = Entalpía_{SIN COMPRIMIR} + Energía Cinética

Como no hay ninguna otra energía, la energía total en ambos casos es la misma y podemos decir que:

Entalpía_COMPRIMIDO  = Entalpía_{SIN COMPRIMIR} + Energía Cinética

O lo que es lo mismo:

Entalpía_COMPRIMIDO  - Entalpía_{SIN COMPRIMIR} = Energía Cinética

Como vemos, la energía cinética depende de como varia la entalpía del gas comprimido al gas sin comprimir; por lo que recordando la fórmula de la variación de la entalpía en función de la velocidad del sonido (Variación de Entalpía = c² x Variación de Masa) podemos escribir finalmente:

Energía Cinética = Masa_COMPRIMIDO x c² – Masa_{SIN COMPRIMIR} x c²

Como en el chorro que sale del tanque el gas ya se descomprimió, la energía cinética vale:

Energía Cinética = Masa_{SIN COMPRIMIR} x v² / 2

Para terminar este análisis tenemos que analizar todavía la energía cinética y para ello tenemos que hacer un pequeño truco.

 

UN TRUCO MATEMÁTICO.

 

Muchas veces, en matemáticas y también en nuestra vida diaria, es conveniente cambiar ciertas cosas por otras que den el mismo resultado. Por ejemplo, si tenemos que multiplicar 2 x 3, podemos sustituir esta multiplicación por la suma de 1 + 2 + 3. En ambos casos el resultado es 6, por lo que no hay ningún error, y esta sustitución nos puede facilitar los cálculos que estemos haciendo. En matemáticas es bastante frecuente cambiar una multiplicación por una suma que dé el mismo resultado; esto facilita el cálculo y, a veces, permite llegar a una solución que de otra forma es imposible.

 

Las sumas de este tipo, en las que los sumandos siguen cierto orden establecido, se llaman series y son de uso frecuente en matemáticas; entre las más usadas están las series de Taylor, de Fourier, del binomio y otras.

 

El truco que haremos a continuación consiste en cambiar la ecuación de la energía cinética por su equivalente en serie del binomio. Como este desarrollo es algo complicado lo escribo enmarcado para aquellos que saben matemáticas y después continuo sin enmarcar dando un resumen para quienes no saben matemáticas. La omisión de la parte enmarcada no afecta al entendimiento de los fenómenos físicos que estamos estudiando.

 

 

 

 

 

Todo esto se resume diciendo que la expresión: Masa_{SIN COMPRIMIR} x v² / 2 se puede reemplazar por su equivalente  Masa_{SIN COMPRIMIR}   x  c²  /  f )  -  Masa_{SIN COMPRIMIR}  x  c² ,  donde la letra f es un factor de corrección, al que llamaremos corrección relativista cuyo valor es:

f  = ( 1 -  (v²/ c²) )^1/2

Reemplazando estos valores:

Cinética  = ( Masa_{SIN COMPRIMIR}   x  c²  /  f )  -  Masa_{SIN COMPRIMIR}  x  c²

Pero, por otra parte, vimos anteriormente que la energía cinética es igual a la variación en entalpía y que esta venia expresada por:

Cinética = Masa_COMPRIMIDO x c² – Masa_{SIN COMPRIMIR} x c²

Comparando estas dos últimas ecuaciones vemos que son muy parecidas y si sustituimos Masa_COMPRIMIDO  por  Masa_{SIN COMPRIMIR}  / f  quedan idénticas; por lo que podemos concluir que:

Masa_COMPRIMIDO = Masa_{SIN COMPRIMIR}  / f

Puesto que la velocidad  v  del cuerpo es menor que la velocidad  c  del sonido, el factor  f  es menor que la unidad, por lo que al poner valores numéricos en las ecuaciones anteriores, veremos que la masa del fluido comprimido es mayor que la masa del fluido sin comprimir. En otras palabras, la masa que cabe en un volumen dado es mayor mientras mas comprimida esté, lo que es evidente.

Podemos invertir el problema y suponer que el gas se mueve a la velocidad v hacia el interior del tanque y que se comprime al entrar a él. Las relaciones matemáticas serán las mismas.

 

LIMITACIONES DEL TRUCO MATEMÁTICO

En el truco matemático que hicimos anteriormente vimos que podíamos sustituir la cantidad 1 / f por la cantidad 1  +  (v² / 2 c² )  +  …… donde los puntos suspensivos significan que hay que sumar otras cantidades pero que estas son muy pequeñas cuando v es pequeña comparada con c, en cuyo caso no hay un error notable al hacer la sustitución. En aviación, si la velocidad v es menos que el 80% de c, podemos considerar que no hay error.

Pero si consideramos velocidades mayores, la diferencia entre los cálculos y los resultados reales se harán cada vez mayores, debido a que no consideramos los otros sumandos de la serie.

Si no consideramos esta limitación y suponemos que la velocidad del móvil es igual a la del sonido y sustituimos valores en las fórmulas que hemos visto:

f  = ( 1 -  (v²/ c²) )^1/2

Masa_COMPRIMIDO = Masa_{SIN COMPRIMIR}  / f

 el factor f se hará igual a cero y la masa comprimida será infinita, es decir, todo el aire se comprimirá en un solo punto.

Peor aun será si consideramos velocidades del móvil mayores a la velocidad del sonido. En este caso los resultados nos darían lo que en matemáticas se llaman números imaginarios, no reales, lo que significaría que es imposible moverse a velocidades iguales o superiores a la velocidad del sonido.

 Sin embargo, sabemos que hay aviones que vuelan a la velocidad del sonido e incluso a velocidades mucho mayores.

Esto nos dice que no podemos aplicar las fórmulas desarrolladas a velocidades mayores al 80% de c y que necesitamos otras formulas diferentes para velocidades mas altas. De hecho las formulas usadas en aerodinámica son distintas para aviones que se mueven a velocidades inferiores a 80% de c (aerodinámica subsónica), para aviones que se mueven entre 80%  y 120% de c (aerodinámica transónica) y los que se mueven a mas de 120% de c (aerodinámica supersónica).

Además de las limitaciones de las fórmulas hay consideraciones físicas que hacen inválidas las fórmulas. Alrededor del 80% de c las ondas sonoras que genera un cuerpo que se mueve en el aire se superponen unas con otras formando lo que se llaman ondas de choque y en ellas el cambio del gas deja de ser adiabático. Una razón más para considerar que las fórmulas anteriores no son válidas.

 

OTRAS LIMITACIONES. FLUIDOS REALES.

 

Si analizamos con más detalle la salida del aire comprimido de nuestro tanque, veremos que la boquilla por donde sale el aire se calienta por su roce con el aire; es decir, algo de la energía del gas se pierde en este roce y la energía cinética será algo menor a la calculada.

 

De igual modo, si el aire circula por un tubo hay un roce con las paredes y si un cuerpo se mueve a través del aire también hay un roce entre la superficie del cuerpo y los corpúsculos de aire con los que entra en contacto.

 

O sea, en todos los movimientos entre fluidos (líquidos o gases) hay una parte de energía que se disipa por roce. A esto se le llama perdidas por fricción.

 

Además, los corpúsculos del fluido chocan y se rozan entre si, lo que produce perdidas por viscosidad. También hay pérdidas por turbulencia y otras causas.

 

En todos los fluidos reales hay pérdidas de estos tipos.

 

Si, adicionalmente, extraemos energía del gas, enfriándolo o haciendo que mueva algún objeto como, por ejemplo, un molino, habrá más energía perdida.

 

En todos los casos la energía cinética del gas será menor que la calculada y,  por lo tanto, tenemos que modificar las fórmulas anteriores para considerar la energía perdida. La energía cinética real mas la energía perdida será igual a la energía cinética que se obtendría si no hubiera pérdidas, por lo que podemos llamar ENERGÍA simplemente a esta suma:

 

Energía = Cinética  + PÉRDIDAS

 

 Y las fórmulas quedarán finalmente como:

 

Energía = ( Masa_{SIN COMPRIMIR}   x  c²  /  f )  -  Masa_{SIN COMPRIMIR}  x  c²

Y también:

Energía = Masa_COMPRIMIDO x c² – Masa_{SIN COMPRIMIR} x c²

También se puede dar el caso contrario; o sea que calentemos o agreguemos energía al gas, por ejemplo con una bomba o un ventilador. En este caso las “PERDIDAS” se convierten en “GANANCIAS” de energía y la energía cinética será mayor.

En todos los casos, para fluidos reales y para procesos con extracción o aporte de energía, habrá que evaluar las perdidas y ganancias y considerarlas en las fórmulas anteriores.

Esta es otra limitación que tenemos que considerar.

No obstante, en muchos casos las perdidas y ganancias son muy pequeñas y podemos hacer caso omiso de ellas sin cometer un error notable; por lo que podremos usar las fórmulas tal como las desarrollamos al principio.

 

LA DENSIDAD

 

Al principio de este trabajo vimos como variaba la temperatura con la densidad en un cambio adiabático y después, por simplicidad y por ser una cosa mas conocida, utilizamos la masa en el desarrollo de las fórmulas, pero en repetidas ocasiones aclaramos que esto es lo que ocurre en una unidad de volumen.

En otras palabras, todo lo anterior nos dice lo que sucede en un espacio fijo, por ejemplo un metro cúbico, al cambiar la temperatura y la velocidad del gas.

 

Algo que dijimos y que es obvio, es que mientras más comprimido está un gas cabe más masa en la unidad de volumen. Es decir vimos cuanta masa cabe en una unidad de volumen.

 

Pero también podemos preguntarnos cuanto volumen ocupa una unidad de masa.

 

Esto es lo que haremos a continuación y para ello pondremos las fórmulas anteriores en función de la densidad:

 

Variación de Entalpía = c² x Variación de Densidad

 

Energía Cinética = Densidad_{SIN COMPRIMIR} x v² / 2

 

Energía = Densidad_COMPRIMIDO x c² – Densidad_{SIN COMPRIMIR} x c²

 

Energía  = ( Densidad_{SIN COMPRIMIR}   x  c²  /  f )  -  Densidad_{SIN COMPRIMIR}  x  c²

 

Densidad_COMPRIMIDO = Densidad_{SIN COMPRIMIR}  / f

 

f  = ( 1 -  (v²/ c²) )^1/2

 

 

DISTANCIAS Y TIEMPOS

 

 

Partiremos ahora de la relación entre densidades:

 

Densidad_COMPRIMIDO = Densidad_{SIN COMPRIMIR}  / f

 

O su equivalente:

 

Densidad_{SIN COMPRIMIR} = Densidad_COMPRIMIDO  x f

 

Ya vimos que si consideramos una unidad de volumen, o sea que los volúmenes son iguales pero las masas son diferentes, esto nos lleva a:

 

           masa_{SIN COMPRIMIR} / Volumen   =  f x ( masa_COMPRIMIDO / Volumen )

 

Que se reduce a:

 

           masa_{SIN COMPRIMIR}  =  f x masa_COMPRIMIDO

 

 

O su equivalente:

 

           masa_COMPRIMIDO  =  masa_{SIN COMPRIMIR} / f

        

 

Consideraremos ahora una unidad de masa, o sea que las masas son iguales pero los volúmenes son diferentes, entonces:

 

           masa / Volumen_{SIN COMPRIMIR}   =  f x ( masa / Volúmen_COMPRIMIDO )

 

Que se reduce a:

 

           Volúmen_COMPRIMIDO  =  f x Volumen_{SIN COMPRIMIR}

 

Recordando que el factor f es menor que la unidad, esto nos dice que una masa comprimida ocupa menos volumen que cuando no está comprimida, lo cual es obvio.

 

Si tenemos un kilo de gas sin comprimir que ocupa, por ejemplo, un metro cúbico, sus medidas son de 1 metro de ancho x 1 metro de alto x 1 metro de largo. La compresión se presenta, fundamentalmente, en la dirección del movimiento, quedando sin alterar las dimensiones transversales. Suponiendo que el gas se mueve en la dirección en que medimos el largo, éste se reducirá a menos de un metro, pero la anchura y la altura seguirán siendo de 1 metro; multiplicando estas dos cantidades que no se alteran obtenemos el Área de la sección transversal del gas en estudio y multiplicando por el largo encontramos el volumen que ocupa antes y después de la compresión:

 

Volumen = Área x Largo

 

Y aplicándolo a la relación de volúmenes que acabamos de ver:

 

Área x Largo_COMPRIMIDO = f x Área x Largo_{SIN COMPRIMIR}

 

Que se reduce a:

 

Largo_COMPRIMIDO = f x Largo_{SIN COMPRIMIR}

 

 

Cabe, ahora, hacernos la pregunta; ¿Cuánto tardan en pasar por algún lugar un kilo de gas comprimido y otro sin comprimir, si ambos van a la misma velocidad?.

 

Respuesta: Como las masas son iguales la diferencia de densidades implica una diferencia en los volúmenes y suponiendo que la sección transversal es la misma, esta diferencia solo puede existir en la dirección en que se realiza el movimiento.

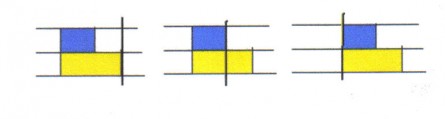
                              t = 0                           t= t_COMPRIMIDO                       t = t_{SIN COMPRIMIR}

 

Movimiento de una unidad de masa sin comprimir (amarillo) y otra unidad comprimida (azul) a través de una sección de referencia.

 

 

Si consideramos los dos kilos en el momento de comenzar a atravesar una línea de referencia en el tubo, ambos comenzaran a entrar al mismo tiempo, pero cuando el Kg. mas corto (comprimido) haya cruzado totalmente la línea (por ejemplo en un tiempo t_COMPRIMIDO), la parte trasera del mas largo (sin comprimir) todavía no habrá cruzado la línea (esto sucederá en el tiempo   t_{SIN COMPRIMIR}). Por lo tanto cada Kg. de fluido tardara tiempos diferentes en cruzar una sección.

 

 

Matemáticamente; como la velocidad (Distancia / Tiempo) es la misma para los dos kilos:

 

 

Largo_{SIN COMPRIMIR} / Tiempo_{SIN COMPRIMIR}  = Largo_COMPRIMIDO / Tiempo_COMPRIMIDO

 

Y substituyendo el valor del Largo_COMPRIMIDO que vimos anteriormente:

 

Largo_{SIN COMPRIMIR} / Tiempo_{SIN COMPRIMIR}  =

 

 f x Largo_{SIN COMPRIMIR} / Tiempo_COMPRIMIDO

 

Llegamos finalmente a:

 

Tiempo_COMPRIMIDO  = f x Tiempo_{SIN COMPRIMIR}

 

 

Es decir, la misma masa, con la misma velocidad, tarda menos tiempo en atravesar una sección del tubo si está comprimida que si esta sin comprimir.

 

 

 

 

 

RELATIVIDAD

 

LA LUZ

 

La primera teoría para explicar que es la luz fue la teoría corpuscular de Newton, que suponía que la luz estaba formada por pequeños corpúsculos que viajaban a gran velocidad. Estos corpúsculos eran emitidos por los cuerpos luminosos.

 

Algunos fenómenos que no se podían explicar con esta teoría hicieron que se sustituyera por la teoría ondulatoria de Huygens, que dice que la luz es una vibración que se transmite a través de los cuerpos.

 

De esta forma la transmisión de la luz es totalmente semejante a la transmisión del sonido, aunque su velocidad es mucho mayor.

 

 Pero en el espacio interestelar, que se consideraba totalmente vacío, no podía haber vibraciones y fue necesario suponer la existencia de un fluido misterioso llamado Éter, que llenaba todo el Universo y por el cual se propagaban las ondas de luz.

 

Este fluido, que no tenía ninguna propiedad física medible, solo servia para justificar las vibraciones ópticas en un medio carente de materia. Las propiedades atribuidas al Éter eran las de un fluido incompresible, es decir un líquido.

 

Cuando Einstein expuso su Teoría de la Relatividad demostró la inutilidad del Éter, que junto con el Flojisto, el Calórico y otros fluidos misteriosos, inventados para explicar algunos fenómenos físicos, pasó a la historia.

 

Sin embargo, al eliminar el Éter quedo la incógnita de explicar la transmisión de la luz en el vacío. Los estudios del mismo Einstein sobre fotoelectricidad dan una pauta para ello; de acuerdo con ellos la luz se comporta como si estuviera formada por corpúsculos, llamados fotones, con masa y otras propiedades físicas perfectamente medibles y por lo tanto tenemos un comportamiento corpuscular de la luz.

 

Actualmente se acepta que la luz tiene un carácter dual; a veces se comporta como corpúsculos y a veces como ondas. La física probabilística considera que la onda es una medida de la probabilidad de encontrar a un fotón en un lugar determinado, con lo que confirma el carácter corpuscular de la luz.

 

ELECTROMAGNETISMO

 

Los estudios sobre electricidad y magnetismo, llevaron a Maxwell a desarrollar su teoría electromagnética y al descubrimiento de que las ondas hertzianas (que transmiten las señales de radio por el espacio), el calor que radian los cuerpos y otras formas de energía radiante, se propagan por el espacio a la misma velocidad que la luz visible. Es decir, esta última es solo una forma más de energía radiante y la diferencia entre las diferentes formas de energía radiante radica solamente en la frecuencia, o sea el número de oscilaciones por segundo, de la onda de radiación.

 

LA CONTRACCIÓN DE LORENTZ

 

Algunos experimentos electromagnéticos y las mismas leyes de Maxwell llevaron a descubrir divergencias entre las teorías anteriores a Maxwell, lo que actualmente se conoce como teoría clásica, y la realidad.

 

En muchos de estos experimentos, los resultados sugerían que el espacio se comportaba como si se hubiera contraído en la dirección del movimiento de un cuerpo. Esto llevó a Lorentz a considerar lo que pasaría si se aceptaba como real esta contracción y un análisis puramente matemático del problema lo llevó a una colección de fórmulas (cuatro en total) que daban las bases para hacer los cambios necesarios para que las fórmulas dieran los resultados coincidentes con los resultados reales. A este conjunto de fórmulas se le conoce actualmente como Transformación de Lorentz.

 

  

 

TEORÍA RESTRINGIDA DE LA RELATIVIDAD

 

Con base en estos experimentos y la explicación de Lorentz, Einstein desarrolló su Teoría Especial, o Restringida, de la Relatividad. Años mas tarde presentó la Teoría General de la Relatividad, de la que hablaremos mas adelante.

 

La Teoría Restringida de la Relatividad parte de dos hechos fundamentales: la validez de la Transformación de Lorentz y la constancia de la velocidad de la luz en el vacío.

 

Para comprender en toda su importancia la Teoría de la Relatividad volveremos a algo que dijimos anteriormente: si un avión se mueve de Norte a Sur en un aire en reposo, las fuerzas son las mismas que si el avión está quieto y el aire se mueve de Sur a Norte. La forma en que analicemos el problema es independiente de los resultados, que deben ser los mismos. Llamamos sistema a la forma en que hacemos el análisis. En un caso el sistema es un avión moviéndose en el aire en reposo y en otro caso el sistema es el avión quieto y el aire moviéndose a su alrededor. En ambos casos el resultado debe ser el mismo.

 

De una manera más general, en cualquier sistema la medida de fuerzas, energías, etc. debe ser la misma. Los físicos parten de este principio, es decir, las leyes del comportamiento de los cuerpos deben ser iguales para todos los sistemas.

 

De acuerdo con esto, la constancia de la velocidad de la luz significa que en cualquier sistema la velocidad de la luz es la misma.

 

Por otra parte, de acuerdo a la teoría de la contracción de Lorentz, un cuerpo en movimiento se contrae en la dirección del moviendo en la cantidad:

 

Largo_{EN MOVIMIENTO} = f x Largo_{EN REPOSO}

Donde f tiene el valor que vimos anteriormente, de: f  = ( 1 -  (v²/ c²) )^1/2

 

Como la velocidad de la luz es la misma en cualquier sistema, tendremos;

 

c = Largo_{EN MOVIMIENTO} / Tiempo_{EN MOVIMIENTO}

 

Y también:

 

c = Largo_{EN REPOSO} / Tiempo_{EN REPOSO}

 

 

Pero para que el resultado de estas dos divisiones sea el mismo, o sea que la velocidad de la luz sea la misma en ambos casos, como el Largo_{EN  MOVIMIENTO} es distinto del Largo_{EN REPOSO} los tiempos deben ser distintos también; es decir, se debe cumplir la condición de que:

 

Tiempo_{EN MOVIMIENTO} = f x Tiempo_{EN REPOSO}

 

De esta forma se cumple la condición de que la velocidad de la luz sea la misma en los dos sistemas.

 

Esto significa que el tiempo no es algo absoluto, sino que cambia de acuerdo con la velocidad del cuerpo en que se mida; es decir, todos los relojes que estén instalados en un cuerpo se moverán mas lentos mientras mas rápido se mueva ese cuerpo y esto no se debe a algún tipo de falla en los relojes sino a algo intrínseco al movimiento del cuerpo. No solo serán más lentos los relojes, sino la vida misma. Esto llevó a plantear lo que se conoce como:

 

LA PARADOJA DE LOS GEMELOS

 

Supongamos dos hermanos gemelos de, por ejemplo, 25 años y pensemos que uno de ellos se embarca en una nave espacial que parte de la Tierra y viaja a una velocidad cercana a la de la luz durante varios años, mientras que el otro permanece en la Tierra.

Como la nave va casi a la velocidad de la luz, los relojes, incluyendo el reloj biológico del gemelo, van más lentos de tal modo que al regresar a la Tierra el gemelo ha envejecido 5 años y tiene una edad de 30 años. Pero como en la Tierra la velocidad es menor, el tiempo pasa más rápido y han transcurrido 65 años. ¡El gemelo en la Tierra tendrá 90 años y será 60 años más viejo que su gemelo!.

 

 

ALGO MÁS DE RELATIVIDAD

 

Resumiendo lo dicho hasta ahora, Einstein estableció lo siguiente:

 

La velocidad de la luz en el vacío es la misma en todos los sistemas, independientemente de a que velocidad se muevan

 

Los cuerpos se contraen en la dirección del movimiento en la cantidad:

 

Largo_{EN MOVIMIENTO} = f x Largo_{EN REPOSO}

 

Las dimensiones transversales (ancho y alto) no se alteran, es decir son las mismas en cualquier sistema.

 

El tiempo se dilata en el cuerpo en movimiento en la cantidad:

 

Tiempo_{EN MOVIMIENTO} = f x Tiempo_{EN REPOSO}

 

Ampliando su análisis Einstein llegó a la conclusión de que la masa también debía cambiar con la velocidad y que este cambio se calcula por la fórmula:

Masa_{EN MOVIMIENTO} = Masa_{EN REPOSO}  / f

 

Es decir, la masa aumenta con la velocidad.

 

Y estableció la siguiente relación para la energía de un cuerpo:

Energía = Masa_{EN MOVIMIENTO} x c² – Masa_{EN REPOSO} x c²

 

Lo que equivale a decir que la energía aumenta al aumentar la masa, misma que aumenta al aumentar la velocidad, o lo que es lo mismo: la energía aumenta con la velocidad.

 

Esta relación entre masa y energía llevó a postular el Principio de Conservación de la Masa y la Energía.

 

Es decir, puesto que una variación de la masa produce una variación de la energía, esto significa que podemos convertir masa en energía o energía en masa, o lo que es lo mismo la masa es una forma de energía.

 

Antes de Einstein la masa era una cosa y la energía otra muy distinta y había dos principios diferentes: el de la Conservación de la Masa y el de la Conservación de la Energía, uno independiente del otro y, en cierta forma, sin ninguna relación.

 

Si prescindimos de la masa en movimiento, la última fórmula se reduce a:

Energía = Masa_{EN REPOSO} x c²

 

O lo que es lo mismo, la popular  E = m c²  que todos conocemos y a la que invocan todos los charlatanes e ignorantes del mundo para justificar sus estupideces involucrando al bueno de Don Alberto en sus barrabasadas.

 

Esta fórmula nos dice que la masa en reposo puede ser convertida en energía.

 

De igual forma, para calcular una fuerza debemos considerar la variación de la masa y tendremos:

 

Fuerza _{EN REPOSO} = Masa _{EN REPOSO} x Aceleración

 

Fuerza_{EN MOVIMIENTO} = Masa_{EN MOVIMIENTO} x Aceleración

 

Y sustituyendo el valor de la masa:

 

Fuerza_{EN MOVIMIENTO} = Masa_{EN REPOSO} x Aceleración / f

 

 

 

 

 

 

AERODINÁMICA Y RELATIVIDAD

 

DOS INTERPRETACIONES DIFERENTES

 

Si en las fórmulas que vimos en el capítulo de AERODINÁMICA sustituimos las palabras “COMPRIMIDO” por “EN MOVIMIENTO” y “SIN COMPRIMIR” por “EN REPOSO”,  vemos que las fórmulas de este capítulo son idénticas a las que escribimos en el capítulo de TEORÍA DE LA RELATIVIDAD.

 

La sustitución es perfectamente válida porque el aire sin comprimir es el aire no alterado, el aire en reposo, de la interpretación aerodinámica y el aire comprimido es el aire alterado por el paso de un cuerpo en movimiento.

 

Tenemos así dos conjuntos de fórmulas idénticas que al aplicarlas a la resolución de problemas nos llevarán a resultados idénticos. Son intercambiables, por así decirlo.

 

Sin embargo, el método por el que se llegó a ellas es diferente y la interpretación de las mismas es distinta. Tenemos, por lo tanto, dos concepciones, dos interpretaciones, distintas que nos llevan a los mismos resultados. Los resultados coinciden, pero ¿Cuál es la interpretación correcta?, ¿La de Einstein o la Aerodinámica?.

 

En mi opinión, la interpretación correcta es la aerodinámica y la de Einstein tiene errores, aunque lleve a resultados correctos. Pero recordemos que en la ciencia no hay “verdades reveladas y absolutas” sino simples suposiciones transitorias que se pueden corregir o modificar al descubrir nuevos hechos con el paso del tiempo y el avance de la ciencia, es decir teorías.

 

De acuerdo con esto, es conveniente comparar las dos interpretaciones para ver cual se apega más a la realidad y dejar que el tiempo decida cual es más convincente.

 

Hagamos comparaciones.

 

 

EL GAS FOTÓNICO

 

Dijimos anteriormente que en la actualidad se considera a la luz como un conjunto de pequeños corpúsculos llamados fotones. Esta vuelta a la teoría corpuscular nos plantea una interpretación diferente de la que existía en la época de Einstein y que, en cierta forma, él no captó, a pesar de que sus ideas fueron las que dieron lugar a ello. Es decir, esto significa que el espacio interestelar no está completamente vacío, si no ocupado por una gran cantidad de fotones que lo recorren en todas direcciones; es decir, el Universo no está completamente vacío, si no lleno por un gas fotónico, al cual, además, hay que añadirle el polvo cósmico, las partículas ionizadas y otros cuerpos que surcan el espacio.

 

La existencia de este gas fotónico interestelar, nos permite determinar su comportamiento en todos los fenómenos físicos, incluyendo la velocidad de propagación de una onda lumínica por leyes similares a las de una onda sonora en un gas.

 

Además, como todos los cuerpos emiten radiaciones, siempre habrá fotones surcando el Universo y no puede haber en él un espacio totalmente vacío. Si consiguiéramos vaciar completamente un recipiente, como si le extrajéramos el aire, se volvería a llenar de fotones provenientes de las paredes del mismo recipiente.

 

Por supuesto que entre un fotón y otro hay un espacio vacío a través del cual se mueven ambos. Recordemos el ejemplo de las moscas dentro de un frasco que vimos al principio; cada mosca ocupa cierto espacio pero se puede mover en todo el territorio en que no hay moscas. Al comprimir el frasco las moscas tienen menos espacio, pero pueden seguir moviéndose.

 

 

LA VELOCIDAD DE LA LUZ

 

La velocidad del sonido cambia con la temperatura. La temperatura de la atmósfera cambia por su interrelación con la superficie terrestre que la calienta o enfría de acuerdo a su proximidad; mientras mas lejos esté el aire de la superficie terrestre menos cambios hay en la temperatura y por lo tanto mas uniformes son la temperatura y la velocidad del sonido. Si el aire llenara todo el Universo, el efecto de la superficie terrestre sería insignificante y puramente local, por lo que podríamos considerar que la velocidad del sonido sería constante en todo el Universo.

 

Aun considerando las variaciones locales, tendremos que tomar como velocidad del sonido el promedio de sus valores locales. En la atmósfera terrestre podemos considerar que la velocidad del sonido es constante en un espacio bastante extenso.

 

Si consideramos la luz como la propagación de una onda en el gas fotónico, podemos decir que en un espacio mucho mas extenso que la atmósfera terrestre la temperatura y la velocidad de la luz se mantienen constantes con solo pequeñas variaciones locales en la cercanía de los cuerpos celestes, por lo que podemos afirmar que la velocidad de la luz en el gas fotónico es constante.

 

 

 

RELACIONES EN AERODINÁMICA

 

En tiempo de Einstein, no se consideró la existencia del gas fotónico y se pensó en un espacio absolutamente vacío y por lo tanto cualquier variación en la densidad o la energía de un cuerpo solo se podrían explicar como variaciones en las propiedades de dicho cuerpo, puesto que era lo único que existía en el espacio vacío. Esto llevó, primero a Lorentz y después a Einstein a considerar que los cuerpos se contraen en la dirección del movimiento, y así poder explicar determinados fenómenos físicos.

 

Si consideramos la existencia del gas fotónico tenemos dos posibilidades diferentes: la contracción del cuerpo (sólido) o la contracción del gas que lo rodea. La experiencia nos dice que un gas se comprime fácilmente, mientras que un sólido se comprime muy poco. Entonces tenemos la posibilidad de explicar las suposiciones de Einstein como variaciones del gas fotónico y no como variaciones de los sólidos que se mueven a través de él.

 

Si adoptamos este punto de vista el problema se reduce a estudiar el movimiento de un sólido a través de un gas (fluido compresible) y podremos aplicar los conocimientos de la aerodinámica normal  a nuestro análisis.

 

Recordemos que todo el desarrollo aerodinámico que vimos anteriormente se basa en los cambios de densidad del gas y recordemos que hicimos dos tipos de consideraciones: ¿Qué sucede en un volumen fijo? y ¿Qué sucede con una unidad de masa?.

 

En un volumen fijo cabe más gas comprimido que sin comprimir (la compresión se debe a la acción del cuerpo que lo altera) por lo que se explica que:

Masa_{EN MOVIMIENTO} = Masa_{EN REPOSO}  / f

 

Este aumento de masa en la unidad de volumen es el motivo de que las fuerzas y energías sean mayores en las partes de gas afectado que en las de gas no alterado, por lo que:

 

Fuerza_{EN MOVIMIENTO} = Masa_{EN REPOSO} x Aceleración / f

 

Y también:

 

Energía_{EN MOVIMIENTO} = Energía_{EN REPOSO} / f

 

Consecuentemente, siempre que consideremos lo que sucede en una unidad de volumen podremos llegar a resultados correctos utilizando las fórmulas anteriores considerando que la masa del gas fotónico aumenta porque hay más gas y no porque el cuerpo que produce la alteración aumente su masa.

 

Por otra parte, si analizamos el comportamiento de una unidad de masa, vemos que se contrae con la velocidad en el sentido del movimiento y mantiene sus dimensiones transversales. Esta contracción hace que su largo sea:

 

Largo_{EN MOVIMIENTO} = f x Largo_{EN REPOSO}

 

 

Y siendo menor su longitud, tardará menos tiempo en recorrer una distancia dada, luego:

 

Tiempo_{EN MOVIMIENTO} = f x Tiempo_{EN REPOSO}

 

Es interesante, en este punto, hacer una comparación entre ambas interpretaciones.

 

Ya dijimos que Einstein considera que los cuerpos en movimiento se contraen en la dirección de éste y que mantienen inalteradas sus dimensiones transversales. Si dos personas (Juan y Pedro) están en reposo pueden comparar sus reglas y ver que son exactamente iguales, por lo que cualquier medida que hagan con ellas será idéntica. Para ambos un metro cúbico medirá 1 metro de ancho, 1 metro de alto y 1 metro de largo.

 

Supongamos que Juan se sube en un tren que viaja en línea recta, mientras Pedro permanece en tierra. Debido a la contracción ocasionada por el movimiento, Pedro verá que el largo del metro cúbico de Juan se reduce, por ejemplo a 70 centímetros, mientras que la anchura y la altura seguirán siendo de 1 metro.

 

Juan debería observar esta alteración en las dimensiones, pero como su regla también está en movimiento sufre una contracción equivalente a la del objeto que va a medir y por lo tanto medirá un largo de 1 metro y no de 70 cm. como hizo Pedro. Esto se debe a que los centímetros de su regla se hicieron chiquitos sin que él tenga forma de darse cuenta.

 

Al cambiar la posición de la regla para medir las dimensiones transversales, ésta se "descontrae" y mide 1 metro de ancho y de alto.

 

Por consiguiente Juan concluye que el cuerpo mide 1 x 1 x 1, tanto si está en reposo como si está en movimiento. El cuerpo no cambia de dimensiones.

 

Juan está midiendo 1 m. cuando Pedro mide 70 cm. ¡Una distancia mayor que la real según Pedro!. Esto le llevaría a calcular velocidades distintas a las de Pedro (distancias distintas entre tiempos iguales). Esto es lo que indujo a Einstein a considerar que el tiempo medido por Juan debería ser mayor que el medido por Pedro, para que las velocidades calculadas por ambos fueran iguales (distancias distintas entre tiempos distintos) y de ahí concluyó que el tiempo de Juan debería ser mayor que el tiempo de Pedro, es decir que había una dilatación del tiempo con el movimiento.

 

La interpretación aerodinámica predice un tiempo menor para recorrer una distancia menor (la de la unidad de masa comprimida) sin necesidad de que los relojes de un cuerpo en movimiento alteren su funcionamiento. Volvemos a la idea de un tiempo absoluto que no cambia con la velocidad. Lo único que cambia es el volumen de una unidad de masa comprimida.

 

Matemáticamente, si:

 

Largo_{EN MOVIMIENTO} = f x Largo_{EN REPOSO}

 

implica una contracción del Largo, ya que f es menor que la unidad, entonces:

 

Tiempo_{EN MOVIMIENTO} = f x Tiempo_{EN REPOSO}

 

debe implicar, también, una contracción del tiempo y no una dilatación, ya que las dos fórmulas son semejantes.

 

Esto parece darle más consistencia a la interpretación aerodinámica.

*

El argumento más sólido a favor de la dilatación del tiempo es la existencia de los “relojes naturales”, es decir de las partículas subatómicas (mesones y demás) que viven más tiempo cuando viajan a altas velocidades que cuando están en reposo. La diferencia entre sus tiempos de vida se ajusta perfectamente al factor de corrección relativista.

 

Pero, también, las energías a alta velocidad y en reposo, son diferentes y su diferencia se ajusta perfectamente al factor de corrección relativista. Para transformarse en otras partículas deben disipar la energía que les sobra y la disipación de esta energía requerirá mas tiempo mientras mas energía deban disipar.

 

Haciendo un parangón bastante burdo: el agua debe enfriarse hasta 0^oC para convertirse en hielo; el agua a 10^oC tiene menos energía que el agua 90^oC y, por lo tanto, la primera debe disipar menos energía que la segunda y, en consecuencia, tarda menos tiempo en solidificar. Podemos considerar que lo mismo sucede con las partículas subatómicas, por lo que, en vez de considerar una dilatación del tiempo, podemos considerar que se requiere mas tiempo para disipar mas energía.

 

Otra de las pruebas que se están llevando a cabo consiste en transportar unos relojes en diferentes vehículos y ver que se atrasan con respecto a los que están en tierra.

 

Básicamente los relojes miden el tiempo que tarda un fotón en ir hasta un espejo y regresar al punto del que salió; si estos dos objetos están fijos el fotón recorre una distancia x para llegar al espejo, pero si se mueven, el fotón recorrerá una distancia mayor para alcanzar al espejo y, consecuentemente, tardará más tiempo; los “latidos” del reloj en movimiento son mas lentos, pero esto no significa que el tiempo se dilate.

 

 

*

 

 

MASA Y ENERGÍA

 

Vimos anteriormente que la fórmula de la energía:

 

Energía = Masa_{EN MOVIMIENTO} x c² – Masa_{EN REPOSO} x c²

 

representa únicamente una variación de entalpías en un proceso adiabático.

 

Esto nos lleva, por una parte a considerar lo que se indica a continuación y, por otra, a considerar algo que llama la atención de todos los que tratan por primera vez con la Teoría de Einstein: Si la energía cinética se calcula por la conocida formula:

 

Energía Cinética = Masa x Velocidad²  / 2

 

¿Por qué la relación de Einstein no aparece dividida entre dos?. La respuesta es obvia si consideramos que se trata de un cambio de entalpía y no de una energía cinética.

*

El hecho de que esta fórmula represente un cambio de entalpía apunta a otra divergencia importante entre ambas interpretaciones: la equivalencia entre masa y energía.

 

En las reacciones químicas normales, en las que no se alteran los núcleos atómicos, hay cambios en la energía potencial que mantiene a los electrones unidos a sus núcleos. En cualquier reacción química hay un cambio en la entalpía, incluso en los cambios de estado (sólido a líquido, etc.) o las transformaciones (alotrópicas) de cristales en el estado sólido.

 

Considerando lo anterior, podemos suponer que, de acuerdo con la teoría aerodinámica, la variación de energía es solamente un cambio en la variación de entalpía y ésta, como vimos anteriormente, depende de la variación de densidad y del cuadrado de la velocidad de la luz.

 

De acuerdo con esto, la masa y la energía son diferentes y no se pueden convertir la una en la otra. La variación de energía se debe a la variación de entalpía y la masa permanece constante, independientemente de que esté comprimida o sin comprimir. Recordemos que la energía es la suma de la energía cinética mas la energía “perdida” que sale del sistema.

 

 

 

 

Pero según Einstein la masa se puede convertir en energía y viceversa. Aun en reposo, la masa puede destruirse y convertirse en energía (la famosa relación E = mc² ).

 

Sin embargo, en la realidad nunca se ha observado este cambio de forma total y se explica diciendo que no se puede violar la Ley de las Partículas Pesadas, que establece que el número de protones y neutrones (partículas pesadas) debe permanecer constante en una transformación nuclear, por ejemplo en la fisión o fusión nucleares.

 

Las partículas pesadas de un núcleo atómico están unidas por fuerzas muy grandes que representan una gran cantidad de energía potencial, por lo que de acuerdo al punto de vista aerodinámico, es esta energía potencial la que se convierte en energía radiante.

 

En la antigüedad se pensaba que en las reacciones químicas, por ejemplo en la combustión de un pedazo de carbón, se destruía la masa. Fue Lavoisier quien probó que esto no era así y postuló el Principio de Conservación de la Masa. Para ello le bastó con quemar el carbón en un recipiente cerrado y comprobar que el peso de las cenizas mas el de los gases producidos era igual al del carbón y el aire del recipiente antes de la combustión. En el caso de las reacciones nucleares, con corpúsculos tan pequeños y energías tan grandes, no es difícil que se le escapen al observador muchos detalles y que pueda pensar que hubo una desaparición de masa que se convirtió en energía.

 

Podemos especular concibiendo el gas fotónico como un conjunto de corpúsculos semejantes a las moléculas de un gas. No se como son estos corpúsculos, quizá correspondan a alguna partícula subatómica como los mesones, los quarks o las cuerdas de la mas reciente teoría. En la duda los llamaremos “fotógenos” (generadores de fotones). Sea cual sea la naturaleza de estos corpúsculos su comportamiento es equivalente a las moléculas de un gas. Podemos suponer, por lo tanto, que varios de estos fotógenos se unen para moverse juntos formando una onda a la que llamamos fotón. El fotón sería, entonces, una colección de fotógenos, más o menos comprimidos, que se distribuirían en una forma semejante a la de las moléculas de un gas en una onda de sonido. De hecho, como sucede en una onda sonora, los fotógenos chocan con otros fotógenos transmitiéndoles su energía, de tal forma que su movimiento se limita a pequeñas oscilaciones y lo que viaja es la energía que pasa de fotógeno a fotógeno.

 

De acuerdo con lo anterior, podemos suponer que en la emisión de energía de cualquier cuerpo hay un desprendimiento de  fotógenos y por consiguiente una reducción en la masa del cuerpo. Para separar estos fotógenos (es decir arrancarlos del cuerpo y darles un movimiento inicial) se requiere cierta cantidad de energía. Pero inmediatamente después de separados, los fotógenos chocan con otros y les transmiten su energía iniciándose así la onda energética que pasará de unos fotógenos a otros. La detección de la onda energética es fácil, pero no así la detección de los fotógenos arrancados del cuerpo, por lo que se puede suponer que la masa se convirtió en energía.

 

De una  manera burda podemos suponer algo semejante a oprimir una esponja dentro de una cubeta de agua; el agua absorbida por la esponja es expulsada al oprimirla y se revuelve con la que está afuera, de modo que es muy difícil determinar que moléculas estaban dentro y cuales fuera.

 

Este es otro punto de discusión: ¿Se convierte realmente la masa en energía o hay un desprendimiento de masa que requiere cierta energía que después se propaga por el gas fotónico?.

 

En este último caso es obvio que la energía requerida es proporcional a la masa “desaparecida” por lo que independientemente de que aceptemos un solo principio de conservación de la masa y la energía o que aceptemos por separado la conservación de la masa y la conservación de la energía, la teoría aerodinámica lleva a los mismos resultados que la teoría de Einstein. En particular me inclino por la separación entre masa y energía, ya que la ecuación de energía se puede interpretar como una diferencia de entalpías.

 

Quizá el nombre de “fotógenos” no sea el más apropiado, puesto que los fotónes están ligados a la fuerza electromagnética y da la impresión de que excluimos a las otras fuerzas fundamentales, que, lógicamente, deben incluirse en la teoría.

 

 

 

EL FACTOR DE CORRECIÓN

 

Este es el punto más importante para determinar cual de las dos interpretaciones es más adecuada.

 

En el desarrollo aerodinámico partimos de la definición clásica de energía cinética y al desarrollarla por la serie del binomio llegamos a la conclusión de que se podía poner la energía cinética en función del factor de corrección relativista siempre y cuando se consideraran velocidades subsónicas inferiores al 80% de c. Para velocidades mayores esto no era válido y había que considerar otras teorías y otras fórmulas.

 

Por el contrario, Einstein parte del supuesto de que el factor de corrección relativista es válido para cualquier velocidad y, de hecho, utiliza la serie del binomio para demostrar que la fórmula clásica de la energía cinética solo es válida a bajas velocidades. De esto concluye que las leyes de Newton son solo una aproximación de unas leyes más generales y que solo son aplicables a baja velocidad.

 

Aceptando la validez universal de la corrección relativista, cuando la velocidad es igual a la de la luz el factor de corrección se hace cero y en consecuencia la masa se hace infinita, la longitud de los cuerpos se anula y el tiempo no transcurre. De todo esto Einstein concluye que no se puede viajar a una velocidad superior a la de la luz y que esta velocidad es un límite de la Naturaleza.

 

Pero si consideramos que la corrección relativista solo tiene validez hasta velocidades del 80% de la velocidad de la luz, debemos considerar que las leyes y fórmulas aplicables a velocidades mas altas son distintas y con ello abrimos la posibilidad de que en el gas fotónico se presenten fenómenos transópticos (con velocidades entre 80% y 120% de c ) y superópticos (con velocidades mayores al 120% de c ), regidos por sus propias leyes. Al no ser aplicables las leyes de los fenómenos subópticos, ni la masa se hace infinita, ni las longitudes se anulan, ni se detiene el tiempo.

 

Se dirá que no hay pruebas experimentales de fenómenos superópticos, pero ¿se han buscado?. El simple hecho de considerar que esto es imposible hace que nadie intente diseñar un experimento en este sentido. Si los ingenieros aeronáuticos hubieran considerado como válidas a cualquier velocidad sus ecuaciones de aerodinámica subsónica nadie habría intentado construir un avión supersónico; afortunadamente había objetos que superaban la velocidad del sonido desde antes del desarrollo de la aerodinámica. Sin embargo, hay al menos un caso en que se encuentran velocidades mayores a la de la luz: el efecto Cerenkov. ¿Se podrán diseñar experimentos similares a este y encontrar velocidades superópticas en el vacío?

 

LA TRANSFORMACIÓN DE LORENTZ

 

Lo que sigue requiere unas matemáticas algo más avanzadas, por lo que lo escribo enmarcado y no es necesario que lo lean todos.

 

Cabe aclarar que Lorentz dedujo sus fórmulas por análisis dimensional mientras que la deducción siguiente se obtiene estudiando el movimiento de una onda en un fluido en movimiento.

 

 

 

 

 

 

 

CONCLUSION

 

La teoría aerodinámica para un fluido compresible (gas) que se mueve a velocidades subsónicas con respecto a un sólido inmóvil, o viceversa, nos proporciona un conjunto de fórmulas idénticas a las de la Teoría de Einstein, por lo que en ambos casos llegaremos a resultados iguales en nuestros cálculos.

 

La Teoría Aerodinámica solo requiere suponer la existencia de un gas fotónico que llena el Universo y ver los efectos que producen los sólidos que se mueven en su interior. Estos efectos se reducen a cambios en la densidad del gas con sus consecuencias de cambios en entalpía. No es necesario suponer contracciones de los sólidos, ni tiempos que cambian con la velocidad, así como tampoco suponer que la masa y la energía son equivalentes.

 

En resumen, la Teoría Aerodinámica de la Relatividad es más sencilla que la Teoría de Einstein y es más acorde a nuestra concepción de los fenómenos físicos.

 

Por sencillez, me inclino por esta interpretación.

 

Pasemos a otro tema.

 

 

 

 

 

 

 

TEORIA GENERAL DE LA RELATIVIDAD

 

LA GRAVEDAD.

 

En su Teoría General de la Relatividad, Einstein aborda el estudio de la Fuerza de Gravedad. Es bien conocido su ejemplo del elevador:

 

Si voy en un elevador que va subiendo y brinco dentro de él, ¿vuelvo a bajar al piso o el piso sube hasta mis pies?; en otras palabras ¿hay una fuerza (de gravedad) que me regresa al piso o no hay ninguna fuerza y si entro nuevamente en contacto con el piso es porque éste ha subido hasta alcanzar mis pies?.

 

Einstein sugiere que la respuesta correcta es esta última. La fuerza de gravedad no existe y mi "caída" se debe al ascenso del elevador. La fuerza de gravedad no es una fuerza real, sinó el efecto del ascenso del elevador, es decir, es una pseudofuerza.

 

Para explicar esta "subida" del elevador, Einstein sugiere que todo el Universo se está expandiendo, por lo que el piso de la Tierra nos alcanza cuando brincamos y, como nosotros mismos nos estamos expandiendo, no podemos

detectar esta expansión. Todo el Universo, todos los objetos contenidos en él, son mas grandes cada segundo que pasa; pero no nos damos cuenta de ello porque nosotros mismos somos parte de esa expansión.

 

¿Cómo podemos detectar esta expansión?.

 

 

EL EFECTO DOPPLER.

 

Si estamos en una lancha parada en mitad del mar, cada ola que llega a la lancha hace que ésta se eleve y luego caiga. El número de veces que la lancha suba (y después caiga) nos da la frecuencia con que las olas llegan a la lancha.

 

Si, en lugar de estar parada en mitad del mar, la lancha avanza hacia las olas, la frecuencia con que encontraremos la cresta de una ola será mayor, porque avanzamos hacia ella al mismo tiempo que ella avanza hacia nosotros.

 

Esto es lo que se llama Efecto Doppler. Si estamos parados en medio del mar las subidas y bajadas de nuestra lancha, o sea la frecuencia con que llegan las olas, es menor que si avanzamos hacia las olas.

 

Por el contrario, si nos alejamos de las olas, la frecuencia con que nos alcanza cada cresta es menor.

 

Si consideramos ondas sonoras en lugar de olas del mar, el sonido depende de la frecuencia; una frecuencia alta produce un sonido agudo, una frecuencia baja produce un sonido grave.

 

Si un coche avanza hacia nosotros tocando el claxon, percibiremos un sonido más agudo que si el coche estuviera estacionado. Y cuando pase junto a nosotros y comience a alejarse, el sonido será mas grave. Esta es una experiencia que casi todos  hemos tenido: al acercarse el coche su claxon suena más agudo; al alejarse suena mas grave.

 

Si consideramos ondas de luz, sucede lo mismo. La luz violeta tiene una frecuencia mayor que la luz roja. Un coche que se acerque a nosotros emitirá una luz que percibiremos más violeta de lo que es; cuando el coche se aleje percibiremos una luz más roja.

 

Esto es lo que, generalmente, se denomina como "corrimiento hacia el rojo", es decir, la aparente aparición de frecuencias mas bajas al alejarnos de la fuente de las emisiones de luz.

 

 

EL EFECTO DOPPLER Y LA EXPANSIÓN DEL UNIVERSO

 

Para verificar la expansión del Universo, el efecto Doppler es fundamental; en efecto, si tal expansión existe, las radiaciones mostraran un "corrimiento hacia el rojo" mas acentuado mientras mas lejanas sean las fuentes de emisión de dichas radiaciones. Esto demuestra que las partes mas lejanas del Universo se alejan a mayor velocidad de sus orígenes, tal como predijo Einstein.

 

Este corrimiento hacia el rojo está confirmado por las medidas experimentales.

 

 EL  BIG BANG

 

El hecho de que el Universo se esté expandiendo constantemente plantea la pregunta de ¿Cuándo y como comenzó a expandirse?.

 

Se acepta actualmente que hace muchos millones de años toda la materia y energía del Universo estaban concentradas en un punto y, de repente, sin saber porqué, hubo una gran explosión y el Universo comenzó a expandirse lanzando la materia y la energía en todas direcciones.

 

Esta es la teoría de la Gran Explosión, el Big Bang en inglés.

 

En nuestros días esta es la explicación mas aceptada; pero no todos están de acuerdo con ella. Algunos suponen que en algún futuro el Universo dejará de expandirse y comenzará a contraerse, siguiendo un proceso eterno de expansiones y contracciones alternativas.

 

Todo esto ha dado lugar a muchas preguntas en la física moderna, tales como ¿Qué produjo el Big Bang, como serán las leyes físicas durante la contracción, cual es la forma del universo?, etc.

 

EL  EFECTO COMPTON

 

Al estudiar el comportamiento de los fotones, se vio que cuando un fotón choca con un corpúsculo, por ejemplo un electrón, hay un intercambio de energía entre ambos y que este intercambio sigue las leyes clásicas del choque elástico entre dos cuerpos (por ejemplo dos bolas de billar). Si el choque es inclinado, tanto el fotón como el electrón cambian sus trayectorias y el ángulo de desviación depende de sus energías y de la variación de estas energías antes y después del choque.

 

Como el electrón tiene una masa y una velocidad, su energía es cinética y se puede medir antes y después del choque. La energía que gana es igual a la energía que pierde el fotón.

 

Como el fotón es energía radiante y no tiene masa, su energía se calcula por la fórmula de Planck:

 

Energía = h x frecuencia

 

Donde "h" es un valor universal llamado Constante de Planck.

El cambio de energía del fotón se detecta por el cambio de frecuencia, o lo que es lo mismo, por el color de la luz.

 

Esto es lo que se llama Efecto Compton.

 

Normalmente los fotones, que viajan a la velocidad de la luz, tienen más energía que los electrones, que lo hacen a menor velocidad. Por lo tanto, en un choque entre un fotón y un electrón, este último ganará energía y el fotón la perderá, por lo que su frecuencia será menor después del choque, o sea la luz se correrá hacia el rojo.

 

EL  BIG BANG ¿DOPPLER O COMPTON?

 

Volvemos, otra vez, a considerar el gas fotónico y la gran cantidad de materia interestelar que se conoce que existe. Un fotón viajando por este Universo no vacío, chocará con otros fotones, con electrones, protones, etc. y en cada choque su luz se correrá hacia el rojo, por el efecto Compton. Mientras más distancia recorra más choques habrá y este corrimiento será más notable.

 

Si no consideramos la existencia del gas fotónico y suponemos el Universo totalmente vacío, la única explicación de porque la luz de las estrellas es mas roja mientras mas lejanas estén, es la del efecto Doppler.

 

Si suponemos que el corrimiento hacia el rojo se debe al efecto Compton, no es necesario suponer la expansión del Universo y podemos buscar otra explicación para la fuerza de gravedad; por ejemplo como resultado de las atracciones y repulsiones entre los corpúsculos negativos y positivos que forman los cuerpos; quizá algo semejante al Enlace Van Der Waals entre átomos de helio.

 

Un estudio mas detallado de la Teoría General de la Relatividad queda fuera de los alcances de este libro. Solo he querido resaltar el hecho de que el corrimiento hacia el rojo puede deberse al efecto Compton y dejo a otros la tarea de determinar las implicaciones de esto. Por lo tanto, aquí pongo el punto final.